Navigation: LaesieWorks Image Compression Homepage This page


Jump to:

LaesieWorks

Image Compression



LESS COMBINATIONS


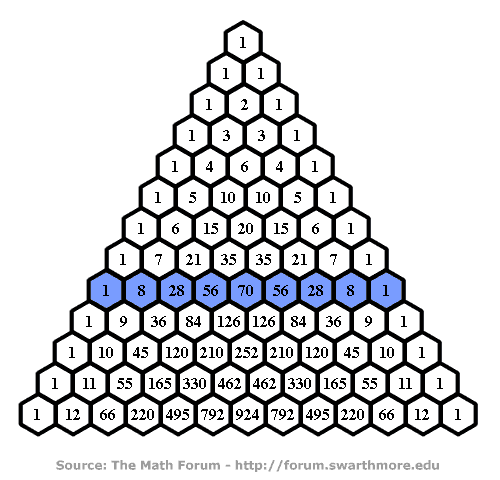
Eight bits have 256 combinations, but if you know that eight out of eight bits are zero, than there's just one combination possible: 00000000. Thus knowing how many bits are 0 and 1, can reduce the amount of possible combinations extremely. The more information there is about a data block, the less combinations are possible. Not just knowing how many zeros and ones there are but knowing more; how many groups of each: 00, 01, 10, and 11 there are (or larger groups), reduces the amount of possible combinations even more.

Next are all 256 combinations of 8 bits, in order of the ratio 1/0

0


1
2
3
4
5
6
7
8


9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36


37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92


93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162


163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218


219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246


247
248
249
250
251
252
253
254


255
 1


1
2
3
4
5
6
7
8


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


1
2
3
4
5
6
7
8


1
 00000000


00000001
00000010
00000100
00001000
00010000
00100000
01000000
10000000


00000011
00000101
00000110
00001001
00001010
00001100
00010001
00010010
00010100
00011000
00100001
00100010
00100100
00101000
00110000
01000001
01000010
01000100
01001000
01010000
01100000
10000001
10000010
10000100
10001000
10010000
10100000
11000000


00000111
00001011
00001101
00001110
00010011
00010101
00010110
00011001
00011010
00011100
00100011
00100101
00100110
00101001
00101010
00101100
00110001
00110010
00110100
00111000
01000011
01000101
01000110
01001001
01001010
01001100
01010001
01010010
01010100
01011000
01100001
01100010
01100100
01101000
01110000
10000011
10000101
10000110
10001001
10001010
10001100
10010001
10010010
10010100
10011000
10100001
10100010
10100100
10101000
10110000
11000001
11000010
11000100
11001000
11010000
11100000


00001111
00010111
00011101
00011110
00011011
00100111
00101011
00101101
00101110
00110011
00110101
00110110
00111001
00111010
00111100
01000111
01001011
01001101
01001110
01010011
01010101
01010110
01011001
01011010
01011100
01100011
01100101
01100110
01101001
01101010
01101100
01110001
01110010
01110100
01111000
10000111
10001011
10001101
10001110
10010011
10010101
10010110
10011001
10011010
10011100
10100011
10100101
10100110
10101001
10101010
10101100
10110001
10110010
10110100
10111000
11000011
11000101
11000110
11001001
11001010
11001100
11010001
11010010
11010100
11011000
11100001
11100010
11100100
11101000
11110000


00011111
00101111
00110111
00111011
00111101
00111110
01001111
01010111
01011011
01011101
01011110
01100111
01101011
01101101
01101110
01110011
01110101
01110110
01111001
01111010
01111100
10001111
10010111
10011011
10011101
10011110
10100111
10101011
10101101
10101110
10110011
10110101
10110110
10111001
10111010
10111100
11000111
11001011
11001101
11001110
11010011
11010101
11010110
11011001
11011010
11011100
11100011
11100101
11100110
11101001
11101010
11101100
11110001
11110010
11110100
11111000


00111111
01011111
01101111
01110111
01111011
01111101
01111110
10011111
10101111
10110111
10111011
10111101
10111110
11001111
11010111
11011011
11011101
11011110
11100111
11101011
11101101
11101110
11110011
11110101
11110110
11111001
11111010
11111100


01111111
10111111
11011111
11101111
11110111
11111011
11111101
11111110


11111111
 1
combination








8
combinations




























28
combinations
























































56
combinations






































































70
combinations
























































56
combinations




























28
combinations








8
combinations

1
combination

For eight bits:

all zero =
1 one =
2 ones =
3 ones =
4 ones =
5 ones =
6 ones =
7 ones =
8 ones =

1 combination
8 combinations
28 combinations
56 combinations
70 combinations
56 combinations
28 combinations
8 combinations
1 combination

PASCAL'S TRIANGLE



Hidden in Pascal's Triangle are a lot of useful answers

The total of each row is equal to a power of 2
Row nr eight = 1 + 8 + 28 + 56 + 70 + 56 + 28 + 8 + 1 = 256 (equal to 2^8)

The formula:
Example A
How many combinations of 8 bits have: eight 0 and zero 1
P = 8! / (8! * 0!)
P = 1
Example B
How many combinations of 8 bits have: six 0 and two 1
P = 8! / (6! * 2!)
P = 28
Example C
How many combinations of 8 bits have: four 0 and four 1
P = 8! / (4! * 4!)
P = 70

More than digital
How many combinations are possible with more than two tones?
Nine tones, represented by nine letters, each appearing once: ABCDEFGHIJ
The amount of combinations is: 9!
9! = 9x8x7x6x5x4x3x2x1 = 362880
But when some tones appear more than once, like: AAAABBCCC
Than the amount of combinations is less than 9! :
9! / (4! * 2! * 3!) = 1260



8 bits (1 color channel pixel):
1
8
28
56
70
56
28
8
1

24 bits (1 RGB color pixel):

1
24
276
2024
10626
42504
134596
346104
735471
1307504
1961256
2496144
2704156
2496144
1961256
1307504
735471
346104
134596
42504
10626
2024
276
24
1

48 bits (2 RGB color pixels):
1
48
1128
17296
194580
1712304
12271512
73629072
377348994
1677106640
6540715896
22595200368
69668534468
192928249296
482320623240
1093260079344
2254848913647
4244421484512
7309837001104
11541847896480
16735679449896
22314239266528
27385657281648
30957699535776
32247603683100
30957699535776
27385657281648
22314239266528
16735679449896
11541847896480
7309837001104
4244421484512
2254848913647
1093260079344
482320623240
192928249296
69668534468
22595200368
6540715896
1677106640
377348994
73629072
12271512
1712304
194580
17296
1128
48
1

A source: Interactive Pascal's Triangle
Special Thanks to Alexandre Iervolino

Giesbert Nijhuis


Back to top


Back to index